概要

超弾性材料は、大きな変形を受けても弾性的に応答する特殊な材料です。非線形の材料挙動と大きな形状変化を示します。その特徴は

100％から700％までの大きな弾性変形を受けることができ、完全に復元可能であること。
ほぼ非圧縮性。つまり、形状は変化しても全体の体積はほぼ一定。
非線形性の高い応力-ひずみ関係。
引張を加えると柔らかくなり、再び硬くなりますが、圧縮を加えるとかなり硬くなります。

多くのポリマーは超弾性的な挙動を示します。例えば、エラストマー、ゴム、その他類似の軟質かつ柔軟性のある材料などです。

超弾性材料は、長期的に高い柔軟性が要求され、高荷重がかかる場合に多く使用されます。代表的な使用例としては、橋梁のエラストマーパッド、レールパッド、自動車のドアシール、自動車タイヤ、流体シールなどがあります。

超弾性理論

有限要素解析では、超弾性材料の大変形時の非線形応答を表現するために超弾性理論が用いられます。超弾性は、有限要素モデルでの使いやすさから人気があります。通常、実験で得た応力-ひずみ曲線データを使用して、理論モデルのパラメータをフィッティングし、材料応答を近似されます。

SimScaleプラットフォームで利用可能な超弾性モデルの選択肢は以下の通りです:

Neo-Hookean (1次)
Mooney-Rivlin(1次)
Signorini (2次)
Yeoh
Ogden (1次、2次、3次)

hyperelastic material setup — 図1: *超弾性*材料の設定

ひずみエネルギー密度関数からの応力-ひずみ関係の計算

超弾性材料の応力-ひずみ関係は通常、ひずみエネルギー密度関数を用いて計算します。以下に簡単な理論的説明を示します。

大きな変形を受ける固体を考えます。元の形状に対して位置$X$ を持つ物体内部の点は、変位ベクトル$u$ によって最終的な形状における位置$x$ に変位します:

$$ x = X + u $$

変形勾配テンソル$F$ は、初期形状と最終形状との関係で次式で与えられます:

$$ F = \frac{ \partial x }{ \partial X } = I + \nabla_{X} u $$

体積の局所的変化$J$ は、その行列式$J = det(F)$ で与えられます。このテンソルは大変形を記述するのに最適な方法ではないことがわかっており、代わりに右のCauchy-Greenテンソルが使われます:

$$ C = F^T F $$

このテンソルは対称的で、その不変量は次式で与えられます:

$$ \mathrm{I}_C = tr(C) $$

$$ \mathrm{II}_C = \frac{1}{2} \Big( tr(C)^2 – tr(C^2) \Big) $$

$$ \mathrm{III}_C = det(C) $$

3番目の不変量$\mathrm{III}_C$ は体積変化に関するもので、次のように書くこともできます:

$$ \mathrm{III}_C = det(F)^2 = J^2 $$

非圧縮性物質の場合、$J = 1$ 。

私たちの目的にとって非常に興味深いのは、右Cauchy-Greenテンソルとその不変量を主伸張比$ \lambda_i $ で表現することです:

$$ \lambda_i = 1 + \varepsilon_i $$

$$ C_{ii} = \lambda_i^2 $$

$$ C_{ij} = 0, i \neq j $$

$$ \mathrm{I}_C = \lambda_1^2 + \lambda_2^2 + \lambda_3^2 $$

$$ \mathrm{II}_C = \lambda_1^2 \lambda_2^2 + \lambda_2^2 \lambda_3^2 + \lambda_3^2 \lambda_1^2 $$

$$ \mathrm{III}_C = \lambda_1^2 \lambda_2^2 \lambda_3^2 $$

ここで、$ \varepsilon_i $ は(元の構成で測定された)主方向の公称ひずみです。伸張比$ \lambda_i $ は変形テンソル$F$ の勾配成分であることに注意してください。

材料の超弾性(第二)Piola-Kirchoff応力テンソル$S$ を右Cauchy-Green変形テンソルに関連付けることができるようなひずみエネルギー密度関数$U$ が存在すると仮定します:

$$ S = 2 \frac{ \partial U }{ \partial C } $$

材料の真応力テンソルは第二Piola-Kirchoff応力テンソルに関係します。これは、右Cauchy-Greenテンソルとひずみエネルギー密度関数で表すことができます:

$$ \sigma_{ij} = -p\delta_{ij} + 2 \frac{ \partial U }{ \partial I_1 } C_{ij} – 2 \frac{ \partial U }{ \partial I_2 } C_{ij}^{-1} $$

ここで、$p$ は純粋な体積変化を引き起こす静水圧外圧で、$ \delta_{ij} $ はクロネッカーのデルタです。非圧縮性の仮定により、$J$ の項は削除されていることに注意してください。

SimScaleで利用可能な材料モデルでは、ひずみエネルギー密度関数は次式で与えられます:

$$ U = C_{10}(I_1 – 3) + C_{01}(I_2 – 3) + C_{20}(I_1 -3)^2 + \frac{1}{2} K (J – 1)^2 $$

$$ I_1 = \mathrm{I}_c J^{-\frac{2}{3}} $$

$$ I_2 = \mathrm{II}_c J^{-\frac{4}{3}} $$

$$ J = \mathrm{III}_c^{\frac{1}{2}} $$

ユーザーインターフェースでは、圧縮性は$D_1$ 定数によって制御されます:

$$ D_1 = \frac{2}{K} $$

利用可能な超弾性モデル（ひずみエネルギー密度関数）

特定の超弾性材料を定義するために適切な材料パラメータを与える前に、超弾性モデルのひずみエネルギー密度関数形式を知っておく必要があります。以下に、SimScaleプラットフォームで利用可能なすべての超弾性モデルのひずみエネルギー密度関数を示します。

Neo-Hookean

上記の定式化で$ C_{01} = C_{20} = 0 $ 、Neo-Hookeanとして最も基本的な形式が得られます:

$$ U = C_{10}(I_1 – 3) + \frac{1}{D_1} (J – 1)^2 $$

Mooney-Rivlin

上記の定式化で$ C_{20} = 0 $ 、次の式で与えられる、Mooney-Rivlinとして知られるNeo-Hookeanの拡張形式が得られます:

$$ U = C_{10}(I_1 – 3) + C_{01}(I_2 – 3) + \frac{1}{D_1} (J – 1)^2 $$

Signorini

Signoriniのひずみエネルギー密度関数は次のように表されます:

$$ U = C_{10}(I_1 – 3) + C_{01}(I_2 – 3) + C_{20}(I_1 -3)^2 +\frac{1}{D_1} (J – 1)^2 $$

Yeoh

Yeohのひずみエネルギーポテンシャルは次式で表されます:

$$U =C_{10}(I_1 – 3) + C_{20}(I_2 – 3)^2 + C_{30}(I_1 -3)^3 +\frac{1}{D_1} (J – 1)^2 $$

Ogden

Ogdenのひずみエネルギーポテンシャルは次の式で表されます:

$$ U =\sum_{i=1}^{N} \frac{\mu_{i}}{\alpha_i} (\lambda_1’^{\alpha_i}+\lambda_2’^{\alpha_i}+\lambda_3’^{\alpha_i}-3)+\frac{1}{D_1} (J – 1)^2$$

ここで

$$N = \text{Order of the Model} $$

$$\lambda_1’^{},\lambda_2’^{},\lambda_3’^{} $$ は偏差主伸張比で定義されます。$\lambda_p $ $ \lambda_p’ = J^{\frac{1}{3}\lambda_p} $

Ogdenモデルを指定する場合、ユーザーはモデルの次数を 1 次から 3 次まで指定することができます。

荷重状態

超弾性材料を完全に特性化するためのパズルの最後のピースは、荷重状態によって決まる伸張比$ \lambda_i $ の定義です。以下のグラフ(Axel Product, Inc.より引用)に示されるように、同じ材料でも荷重のかかり方によって挙動が異なります。一般的な試験では、試験片に所望の荷重状態を与え、応力-ひずみ関係を測定します。

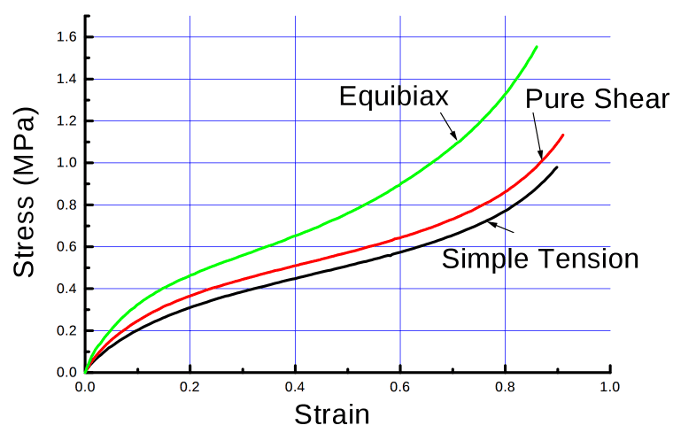
typical hyperelastic material stress-strain curves — 図 2: 超弾性応力-ひずみ曲線の例

一軸引張

非圧縮性材料の一軸引張荷重の場合、試験片は一軸に沿って荷重を受けます。伸張比は次式で与えられます:

$$ \lambda_1 = 1 + \varepsilon $$

$$ \lambda_2 = \lambda_3 = \lambda_1^{ -1/2 } $$

二軸引張

非圧縮性材料の等軸引張荷重の場合、試験片は同じ大きさの2つの垂直軸に沿って荷重を受けます。伸張比は次式で与えられます:

$$ \lambda_1 = \lambda_2 = 1 + \varepsilon $$

$$ \lambda_3 = \lambda_1^{ -2 } $$

純せん断

非圧縮性材料の純せん断荷重の場合、試験片は2つの垂直方向(一方は引張、他方は圧縮)に荷重を受けます。平面ひずみ条件が仮定されるため、無負荷方向には変形しません。伸張比は次式で与えられます:

$$ \lambda_1 = 1 + \varepsilon $$

$$ \lambda_2 = 1 $$

$$ \lambda_3 = \lambda_1^{ -1 } $$

実験データからの材料パラメータの取得

材料特性を実験的な応力-ひずみ曲線に適合させるためには、上に示したすべての関係を考慮に入れる必要があります。方程式を組み合わせて応力をひずみで表し、その関数を試験データに最小二乗法でフィッティングさせてモデルの定数を決定します。ほとんどの場合、フィッティングの精度はモデルの次数が高くなるにつれて高くなります。

例として、Signoriniモデルの非圧縮性一軸応力-ひずみ関係を考えてみましょう:

$$ U = C_{10}(I_1 – 3) + C_{01}(I_2 – 3) + C_{20}(I_1 -3)^2 +\frac{1}{D_1} (J – 1)^2 $$

一軸伸張の定義を使うと、真応力は次のように書けます:

$$ \sigma_{11} = -p + 2 \frac{\partial U}{\partial I_1} \lambda^2 – 2 \frac{\partial U}{\partial I_2} \lambda^{-2} $$

となります:

$$ \sigma_{22} = -p + 2 \frac{\partial U}{\partial I_1} \lambda^{-1} – 2 \frac{\partial U}{\partial I_2} \lambda = 0 $$

圧力項を取り除き、因数分解し、導関数を実行すると、次のようになります:

$$ \sigma_{11} = 2 ( \lambda^2 – \lambda^{-1} ) \Big[ \frac{\partial U}{\partial I_1} + \lambda^{-1} \frac{\partial U}{\partial I_2} \Big] $$

$$ \frac{\partial U}{\partial I_1} = C_{10} + 2 C_{20} (I_1 – 3) $$

$$ \frac{\partial U}{\partial I_2} = C_{01} $$

これで、$ C_{10}, C_{01}, C_{20} $ 定数を決定するための最小二乗フィッティングアルゴリズムに入力すべき応力-ひずみ関数が完成します。

重要

伸張比、ひずみ、応力の関係についてこの手順で定義した式を使用する場合、パラメータカーブフィッティングの入力量は公称(工学)ひずみと真応力でなければならないことに注意してください。

同様の式は、等軸引張の場合にも導くことができます:

$$ \sigma_{11} = 2 ( \lambda^2 – \lambda^{-4} ) \Big[ \frac{\partial U}{\partial I_1} + \lambda^{2} \frac{\partial U}{\partial I_2} \Big] $$

また、純せん断の場合も同様です:

$$ \sigma_{11} = 2 ( \lambda^2 – \lambda^{-2} ) \Big[ \frac{\partial U}{\partial I_1} + \frac{\partial U}{\partial I_2} \Big] $$

非圧縮性の条件により、$D_1$ パラメータはこの手順では推定できないことに注意してください。推奨されるのは、弾性関係を用いて近似値を与えることです:

$$ D_1 = \frac{ 1 – 2 \nu }{ C_{01} + C_{10} } $$

ほとんど非圧縮性の材料の場合、$ \nu $ の値は0.5に近いです。

SimScaleでの材料パラメータ付与

特定のモデルの材料定数が実験データとの良好なフィットから得られたら、SimScaleの材料特性の下にある指定された材料モデルにこれらの定数を入力することができます:

入力される定数は、フィッティングで得られた$C_{10}$ 、$C_{01}$ 、$C_{20}$ の適切な組み合わせです。
得られた定数値のいずれかが他の定数よりも比較的大きい場合、シミュレーション後に得られる結果が正確でない場合があることが確認されています。
非圧縮性の場合
- $D_1$ の推奨値$\nu$= 0.499 を第一近似値として使用します。
- $D_1$ の値を小さくして、より正確な結果を得ます。これにより、材料は完全に非圧縮性に近づきます。
- 収束の問題が発生した場合は、$D_1$ に小さい値を与えるのを止めてください。
- $D_1$ には少なくとも 1×10 ^{- 10}の値を与えてください。

最終更新日: 2025年1月7日

概要