概要
純粋な塑性材料モデルは、塑性が発生した後の材料挙動を記述します。この時点で、固体材料は荷重を受けると不可逆的な変形を起こします。例えば、固体の金属が曲げや叩きによって成形されるような場合です。
実際には、ほとんどの材料は降伏点によって弾性領域と塑性領域が分かれており、降伏点を過ぎると 応力-ひずみ曲線は 非線形になります。鋼の典型的な応力-ひずみ曲線を以下に示します:
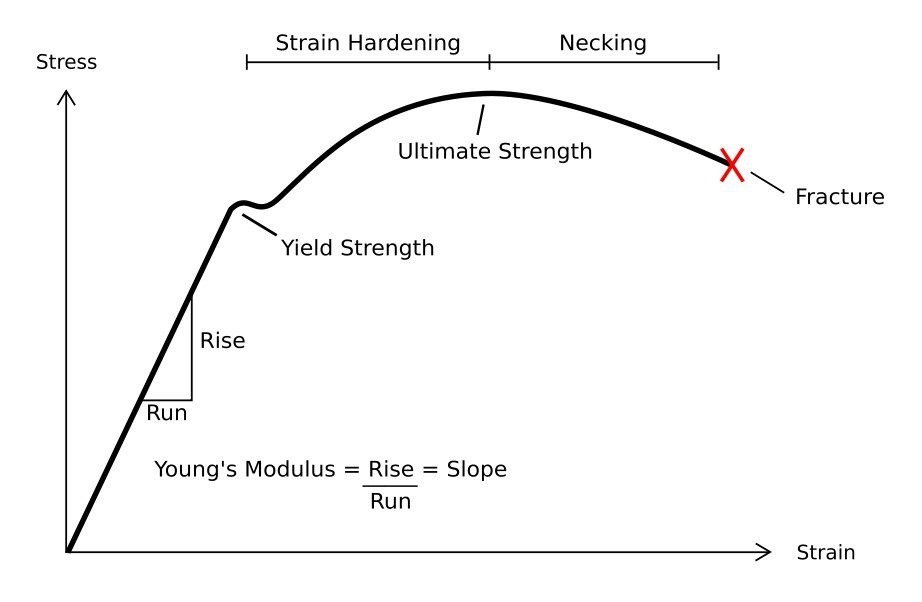
そのため、SimScaleではこのような材料を弾塑性材料としてモデル化することができます。弾塑性材料モデルには様々な用途があるため、衝撃荷重、高圧、高温などの過酷な条件下での材料の挙動予測に特に有効です。
また、設計上ある程度の塑性変形が許容される用途もあります。このような場合、まず材料の 線形弾性挙動を使用してシミュレーションを実行します。応力が降伏強度を超える場合は、塑性材料挙動で追加解析を行います。
重要
弾塑性材料挙動を定義できるのは、以下の解析タイプのみです:
- 非線形静解析
- 動解析
- 非線形熱応力解析
弾塑性モデル
弾塑性領域を持つ材料は、マルチリニアまたはバイリニアとしてモデル化することができます。
マルチリニアモデル
材料をマルチリニアとしてモデル化することは、その特性が引張試験から得られる応力-ひずみ曲線と同じであることを確立することを意味します。このモデルでは、ひずみ硬化曲線は非線形挙動に接するいくつかの直線によってプロットされます。したがって、マルチリニアモデリングでは、材料はできるだけ現実に近い挙動を示します。
バイリニアモデル
バイリニア硬化モデルはマルチリニアモデルと似ていますが、材料の挙動履歴全体を考慮していません。このモデルも応力-ひずみ曲線で記述され、材料の特性評価に必要な係数はヤング率と塑性相弾性率です。塑性相弾性率がヤング率の99%を占める場合、バイリニアモデルは線形弾性解析をシミュレートします。塑性相弾性率が1%および/または0の場合、バイリニアモデルは完全塑性の挙動をシミュレートします。

図2に示すように、バイリニア弾塑性モデルは、シミュレーションにおいて形状や荷重の点で複雑さがない場合、材料の挙動を予測するのに十分であると仮定することができます。
クイックヒント
バイリニア弾塑性モデルは、シンプルで迅速なモデリングが可能です。しかし、より正確さが必要な場合や複雑なモデルの場合は、マルチリニアを使用することをお勧めします。
バイリニア弾塑性モデルを選択した場合でも、SimScaleは硬化モデルのオプションとして完全塑性も提供します。一般的に、完全塑性は実際の材料挙動を単純化したものであり、以下の2つの状況でのみ適用可能です:
- 材料がひずみ硬化しない場合;
- 材料が繰り返し荷重を受けない場合。
SimScaleでの弾塑性材料の定義
工学的応力-ひずみと真の応力-ひずみ
実際のほとんどの材料パラメータは工学的応力-ひずみとして提供されますが、SimScaleでは材料の薄肉化に正確に対応するために真の応力-ひずみ材料特性を必要とします。
工学的応力ひずみと真の応力ひずみ
延性材料の場合、材料試験中にプローブが薄くなることがあります。応力は$$ Stress=\frac{Force}{Cross \ section} = \frac{N}{m^2} \tag{1}$$として計算されるため、2つの材料パラメータを得ることができます。初期断面を基準とする工学応力と、材料の真の断面を基準とする真応力です。
工学応力-ひずみデータを真の応力-ひずみに変換するには、以下の公式を使用します。
\( \sigma_t = \sigma_e*(1+\epsilon_e) \tag{2} \)
\( \epsilon_t = ln(1+\epsilon_e) \tag{3} \)
ここで
\( \sigma_t \) = 真の応力
\( \epsilon_t \) = 真のひずみ
\( \sigma_e \) = 工学応力
\( \epsilon_e \) = 工学ひずみ
\(ln\) = 自然対数
また、工学応力-ひずみ曲線の代わりに、真の応力-塑性ひずみ曲線として材料データが提供されることもあります。このような場合、これも真応力-真ひずみに変換する必要があります。このデータの変換には次の式 4 を使用します。
\( \epsilon_t = \epsilon_p + \frac{\sigma_t}{E} \tag{4} \)
ここで
\( \epsilon_p \) = 塑性ひずみ
\( E \) = ヤング率
SimScaleでの設定
弾塑性材料を定義するには、以下の手順に従ってください:
- シミュレーションツリーの 材料 タブに移動します。 材料挙動 を 弾塑性に 変更します。
- 材料挙動を選択したら、弾塑性モデル (マルチリニア または バイリニア )を選択します。マルチリニアを選択したら、応力-ひずみ曲線のデータを入力する必要があります。応力-ひずみ曲線は 真の応力 対 真のひずみである ことに注意してください。
- ユーザーが材料をバイリニアに設定した場合は、この記事で説明したことを考慮して、完全塑性モデルかひずみ硬化モデルかを決定すればよいだけです。
- 図3は、ユーザーがマルチリニア、完全塑性、バイリニアとしてモデル化した場合の、弾塑性材料であるアルミニウムの例を示しています:

図4から、サンプルの引張試験によって得られた実際の応力-ひずみ曲線を見ることができます。
マルチリニアモデルを選択すると、応力-ひずみ曲線上の一連のデータ点とその座標が定義されます。これらの点は手動で入力することができます。また、任意のテキストエディタで、点座標を含むカンマ区切りの.csvファイルを作成することも可能です(カンマの後にスペースを入れません): ひずみ 、 応力 。この.csvファイルはSimScaleにアップロードできます。
重要
マルチリニアモデルを使用する場合、ソルバーは系列の最初の点を降伏点とみなします。図4を参考にすると、これは.csvファイルの構造になります:
応力-ひずみ曲線を適切に捉えるには、十分なデータ点を追加するようにしてください。2点間では、値は線形補間されます。
-
応力-ひずみ曲線を保存した後、応力-ひずみデータに従って ヤング率を 調整します。 ヤング 率は降伏点における応力とひずみの値を割ることで与えられます:
$$E = \frac {\sigma_{yield}}{\epsilon_{yield}} \tag {5}$$
この例の値を式(5)に入力すると、次のようになります:
$$E = \frac {1.94e8}{2.75e(-3)} = 7.05e10 \ Pa \tag {6}$$
ヤング率の計算値を誤ると、解が発散する可能性があります。
注
このモデルはセラミックスやコンクリートのような脆性材料には適しません。アルミニウムや鋼のような延性で等方性の材料にのみ適用できます。
関連するプロジェクト
最終更新日2024年1月11日