概要
線形弾性材料は、固体の変形を解析するために使用される数学モデルです。物体に加えられる力とそれに対応する変形の関係を計算するのに役立ちます。言い換えれば、材料の応力とひずみの関係です。
変形過程が線形で弾性的であるとみなされるためには、以下の条件を満たす必要があります:
- 材料のひずみから見た変形が小さいこと。
- 荷重を取り除くと、材料は自然に元の変形していない形状に戻ります。言い換えれば、材料の応力レベルが降伏強度の限界に達していないこと。
- 変形の大きさは加えられた荷重に比例します。
線形弾性材料は、バネのフックの法則の一般化と見ることができます:
$$ F = Ku \tag{1}$$
ここで
- \(F\) :バネにかかる引張力
- \(u\) :バネの伸び
- \(K\) :剛性定数で、材料と形状によって決まるばねの特性です。
剛性の形状依存性を取り除くために、一般化のために力と変形の関係を応力とひずみで表現します:
$$ \sigma = \frac{F}{A} \tag{2}$$
$$ \varepsilon = \frac{u}{L} \tag{3}$$
ここで
- \(\sigma\) :引張荷重を受けた角柱の法線応力(単位面積当たりの力)
- \(\varepsilon\) :材料のひずみ(単位長さあたりの変形量)
- \(A\) :荷重に垂直な物体の断面積
- \(L\) :荷重と変形の方向における物体の長さ
これらの項を用いると、一次元の線形弾性関係は次のように表せます:
$$ \sigma = E \varepsilon \tag{4}$$
ここで、\(E\) は材料のヤング率で、応力とひずみの比例関係は以下のように表されます:
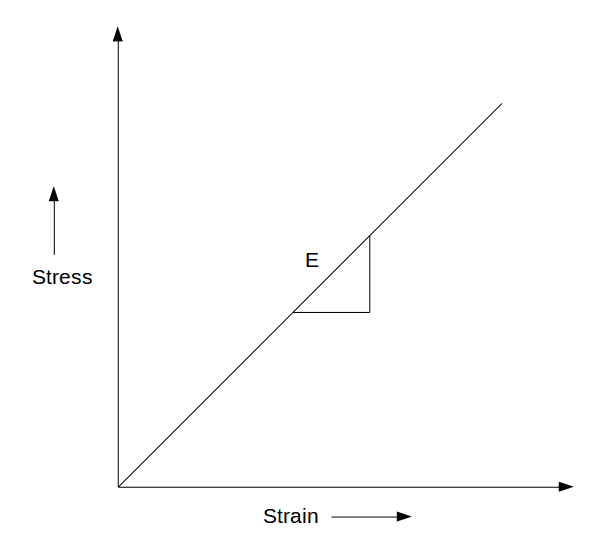
三次元の線形弾性材料
空間内の多方向から荷重を受ける固体物体の一般的なケースにおいては、上述した一次元の関係では変形を説明するのに十分ではありません。3次元では、応力とひずみはテンソル量として表されます:
$$ \sigma = \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{yy} & \tau_{yz} \\ \tau_{zx}& \tau_{zy} & \sigma_{zz} \end{bmatrix} \tag{5} $$
$$ \varepsilon = \begin{bmatrix} \varepsilon_{xx} & \frac{1}{2}\gamma_{xy} & \frac{1}{2}\gamma_{xy} \\ \frac{1}{2}\gamma_{yx} & \varepsilon_{yy} & \frac{1}{2}\gamma_{yz} \\ \frac{1}{2}\gamma_{zx} & \frac{1}{2}\gamma_{zy} & \varepsilon_{yy} \end{bmatrix} = \frac{1}{2}(\nabla_X u + \nabla_X u^T) \tag{6} $$
ここで、\(\nabla_X\) は変形していない構成で計算された勾配演算子であり、\(u\) は材料の変形のベクトルです:
$$ u = \begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix} \tag{7} $$
応力-ひずみ関係の一般形は次のように書けます:
$$ \sigma = \frac{E}{1+\nu} \Big( \varepsilon + \frac{\nu}{1 – 2\nu} Tr(\varepsilon) I \Big) \tag{8}$$
またはひずみについて解くと
$$ \varepsilon = \frac{1 + \nu}{E} \Big( \sigma – \frac{\nu}{1 + \nu} Tr(\sigma) I \Big) \tag{9}$$
ここで、\(\nu\) はポアソン比であり、法線応力と直角方向の変形を関係づけます。ここでは、材料が等方的で均質であると仮定しています。これは、\(E\) や\(\nu\) などの材料特性が位置や方向に対して定数であることを意味します。
SimScaleでの線形弾性材料の定義
構造解析に線形弾性材料を適用するには、以下のパラメータを指定する必要があります:
ワークベンチの「Materials」で「Material behavior」を「Linear elastic」に設定し、パラメータを設定し、ボリュームに割り当てます:
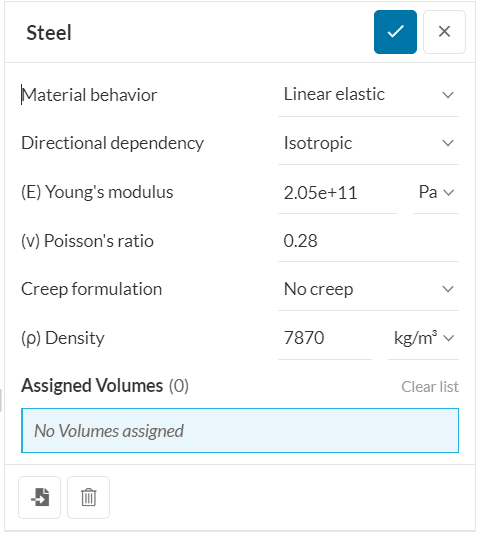
線形弾性領域を超える材料
関連プロジェクト
最終更新日:2024年1月7日