概要
クリープとは、時間の経過に伴う固体材料における非弾性的で不可逆的な変形のことです。構造物の寿命を制限する要因であり、応力、ひずみ、温度、時間などの変数に依存します。この依存性は次のようにモデル化できます:
$$ \begin{equation}\label{creep_dependency_eq}
\dot{\mathbf{\epsilon}}_{cr} = f(\sigma,\epsilon,T,t) \end{equation} \tag1$$
クリープは、金属やガラスなど、あらゆる結晶材料で発生します。クリープは材料の挙動に様々な影響を及ぼし、最終的に以下のような問題を引き起こす可能性があります: [NAFEMS_HT21]
- 不均衡な変形は座屈や破損につながります。可動部品のある機械では、隙間が小さくなり、摩擦摩耗につながる可能性があります。
- ボルト部品の接続は、プレストレスの緩和により、時間の経過とともに緩むことがあります。この緩和は、ケーブル、ガスケット、フランジでも発生する可能性があります。
- 過度の熱と負荷サイクルは、亀裂の進展を促進し、部品の損傷、ひいては故障につながる可能性があります。
このように非常にさまざまな要因があるため、特定の状況におけるクリープの影響は非常に複雑になる可能性があります。クリープ解析を実施することで、これらの影響の影響を評価し、部品の寿命を見積もることができます。特に、商業プラントや軍事プラントのタービンの高温部では、設計プロセスやコストの最適化にとって重要な要素となります。
クリープの3段階
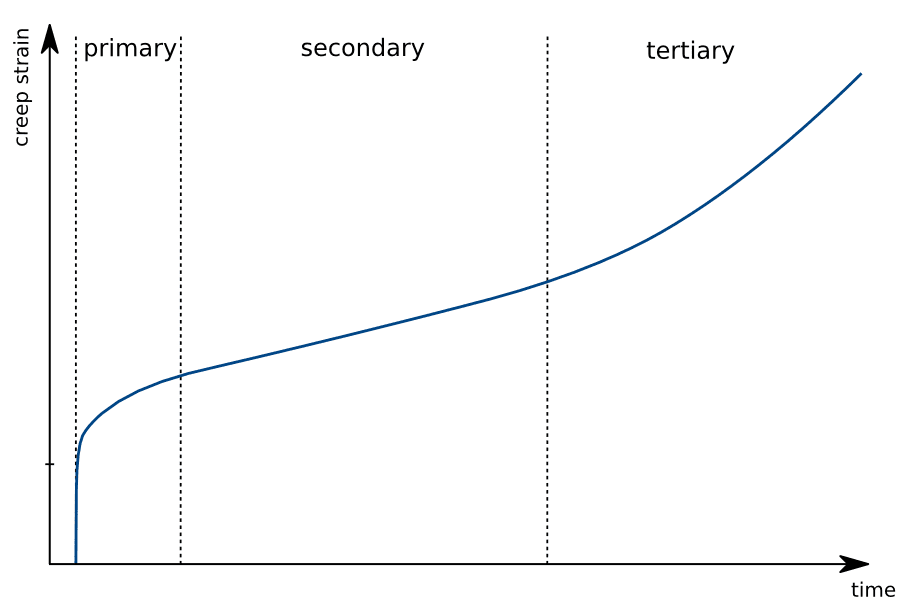
クリープは、一次クリープ、二次クリープ、三次クリープの3つの段階に分けることができます:
一次クリープ (\(-1 < m < 0\))は、初期化時に無限大のクリープ速度で 急速に開始します。ここで、\(m\) は時間指数(方程式のひずみ速度形式の場合)です。一定時間後に発生し、常に減速します。これは荷重を加えてから最初の1 時間持続し、経時的な緩和を計算する上で不可欠です。
二次クリープ (\(m = 0\))は、一次クリープの直後に起こります。ひずみ速度は長時間にわたって一定になります。
三次クリープ 段階のひずみ速度は、破壊に至るまで急速に増大し ます。これは短期間で発生するため、あまり注目され ません。そのため、SimScaleプラットフォームでは一次クリープと二次クリープのみをモデル化しています。
クリープひずみの計算
クリープひずみ方程式は、相加ひずみ分解に基づいています:
$$ \begin{equation}\label{strain_decomposition}
\mathbf{\epsilon}_{tot} = \mathbf{\epsilon}_{el} + \mathbf{\epsilon}_{pl} + \mathbf{\epsilon}_{cr} \end{equation} $$
$$ \begin{equation}\label{small_strain_hypo} \mathbf{\sigma} = \mathbf{D} : \mathbf{\epsilon}_{el} \end{equation} $$
$$ \begin{equation}\label{creep_strain_eq} \dot{\mathbf{\epsilon}}_{cr} = \frac{3}{2} \dot{\epsilon^c} \frac {\tilde{\mathbf{\sigma}}}{\sigma_{eq}} \end{equation} $$
ここで
- \(\mathbf{\epsilon}_{tot}\) :全ひずみテンソル
- \(\mathbf{\epsilon}_{el}\) :弾性ひずみテンソル
- \(\mathbf{\epsilon}_{pl}\) :塑性ひずみテンソル
- \(\mathbf{\epsilon}_{cr}\) :クリープひずみテンソル
- \(\mathbf{\epsilon^c}\):等価クリープひずみ
- \(\tilde{\mathbf{\sigma}}\):偏差応力テンソル
- \(\sigma_{eq}\):等価応力
- \(\mathbf{D}\):弾性テンソル
- 量の上のドットは変化率を表し、例えばクリープテンソルのひずみ率です。
- \( \dot{ \epsilon }_{cr} \)
弾性ひずみ\(\mathbf{\epsilon}_{el}\) は荷重をかけた直後に発生し、式 1 の弾性テンソル\(\mathbf{D}\) を介して応力と結びつきます。塑性ひずみ\(\mathbf{\epsilon}_{pl}\) は過大な荷重から生じ、不可逆的です。クリープひずみテンソルは、等価クリープひずみ\(\mathbf{\epsilon^c}\) 、偏差応力\(\tilde{\mathbf{\sigma}}\) 、および等価応力\(\sigma_{eq}\) で計算できます。偏差応力\(\tilde{\mathbf{\sigma}}\) はボディの歪みを引き起こし、応力テンソルを相加的な等方性成分と偏差性成分に分割した結果生じます。
等価クリープひずみの計算
SimScaleでは、クリープひずみ速度式として定義された基本的な クリープ則タイプを利用できます:
べき乗則 またはBailey-Norton則です:
$$ \dot{\epsilon^c} = A \cdot \sigma^{n} \cdot t^m \cdot \epsilon^{k}$$
ここで
- \(A\):問題に依存する定数
- \(n\):クリープ応力指数 \(1 <= n <= 10\)
- \(m\):時間指数 \(-1 < m <= 0\)
- \(k\):クリープひずみ指数
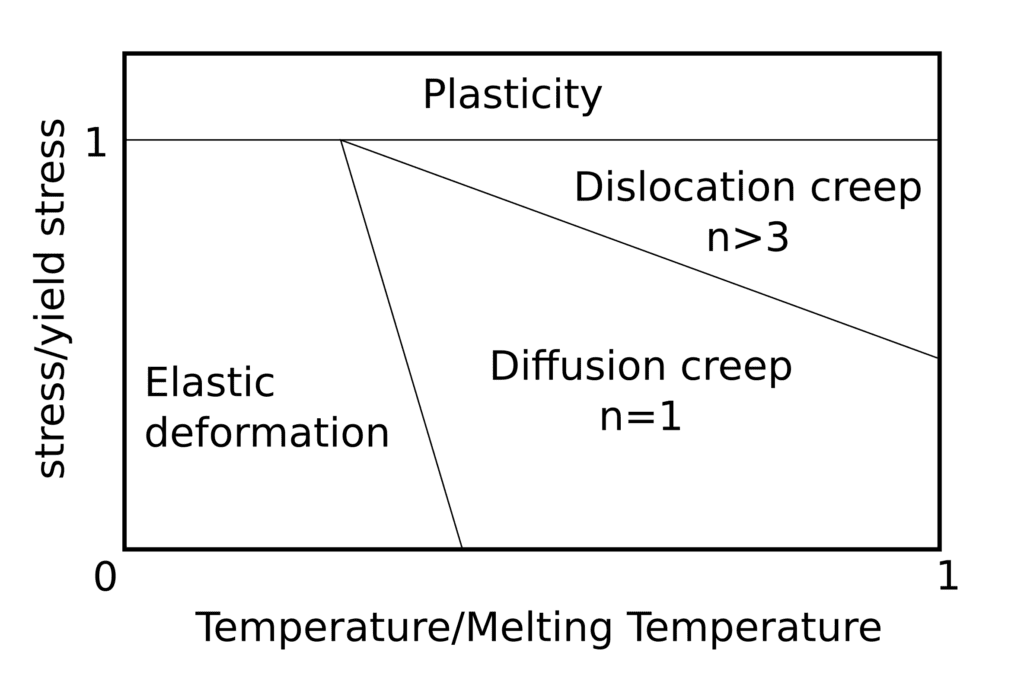
クリープ応力指数は、温度と応力レベルに依存し、Ashbyの変形機構領域図を用いて決定することができます。
これらの基本法則に基づき、現在プラットフォームでは3つの異なるクリープ公式が利用可能です:
Norton (ノートン則)
この定式化では、クリープひずみ速度は応力のみに依存し ます。したがって、\(m\)と\(k\)はゼロに等しくなります:
$$ \dot{\epsilon^c} = A \cdot \sigma^{n}$$
Time hardening (時間硬化)
この定式化では、クリープひずみ速度は時間にも依存します:
$$ \dot{\epsilon^c} = A \cdot \sigma^{n} \cdot t^m$$
Strain hardening (ひずみ硬化)
この公式では、クリープひずみ速度は応力とクリープひずみに依存します。(SimScaleのプラットフォームでは便宜上、\(k\)を\(m\)と呼びます)。
$$ \dot{\epsilon^c} = A \cdot \sigma^{n} \cdot (\epsilon^c)^k$$
SimScaleでのクリープ材料の定義
クリープ挙動は線形弾性および弾塑性材料モデルに適用できます。モデルを定義するには、以下の手順に従ってください:
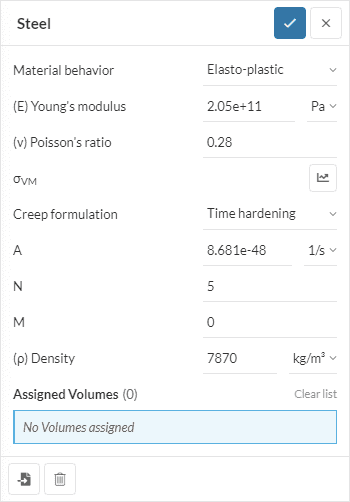
- シミュレーションツリーの Materials(材料) タブに移動します。 材料挙動がLinear elastic(線形弾性) または Elasto-plastic(弾塑性) であることを確認します。
- 問題に適した クリープ定式化を選択します。
- 選択した定式化に従って\( A, N, M \) パラメータを入力します。
重要
- クリープ定式化パラメータ\((A, m, n)\) および\((\epsilon_0^c, \sigma_0)\) は、クリープ則の速度形式に関して上式にて定義されます。
-
文献や材料メーカー、試験データから得られたパラメータを変換する際には、単位系を統一することが重要です。多くの場合、クリープパラメータは長さ(\(mm\) )、応力(\(MPa\) )、時間(hour)に関連して与えられます。時間硬化またはひずみ硬化処方のパラメータ\(A\) の変換方法の例は次の通りです: \(A_{SI} = \frac{1}{3600} \cdot \frac{1}{3600^m} \cdot \frac{1}{10^{6n}} \cdot A_{MPa\;h}\)
- 特に一次クリープが観察される場合、クリープ挙動を正しく捉えるために時間ステップを十分に精緻化することが非常に重要です。そのため、Code_Asterの自動時間ステップ(英語)のフィールド変更基準を使用することをお勧めします。
関連プロジェクト
- 検証ケース:3次元三軸荷重二次クリープ(NAFEMS Test 6(a))
- 検証ケース:3次元三軸変位二次クリープ(NAFEMS Test 6(b))
- 検証ケース:3次元三軸荷重一次クリープ(NAFEMS Test11)
最終更新日2024年3月7日