Linear elastic (弾性材料)概要
ヤング率または縦弾性係数は、線形弾性材料の機械的特性です。固体材料の応力とひずみの関係を定義し、次式で与えられます:
$$ \sigma = E \varepsilon $$
ここで
- \(E\) :材料のヤング率
- \(\sigma\) :応力
- \(\varepsilon\) :ひずみ
ひずみは無次元量であるため、ヤング率の単位は(\(Pa, psi \)) です。この関係から、ヤング率は応力とひずみの比であることがわかります:
$$ E = \frac{ \sigma }{ \varepsilon } $$
物理的に言えば、ヤング率は材料の剛性を示す尺度です。部品の全体的な剛性は幾何学的形状にも依存するため、材料を測定するには形状に依存しない特性が必要です。
線形弾性材料のヤング率
固体材料は、加えられた荷重が取り除かれた後、自然に元の形状に戻ることができる場合、弾性と呼ばれます。一方、変形過程において応力とひずみの比が一定であれば、ヤング率も一定となり、その材料は線形弾性であると考えられます。
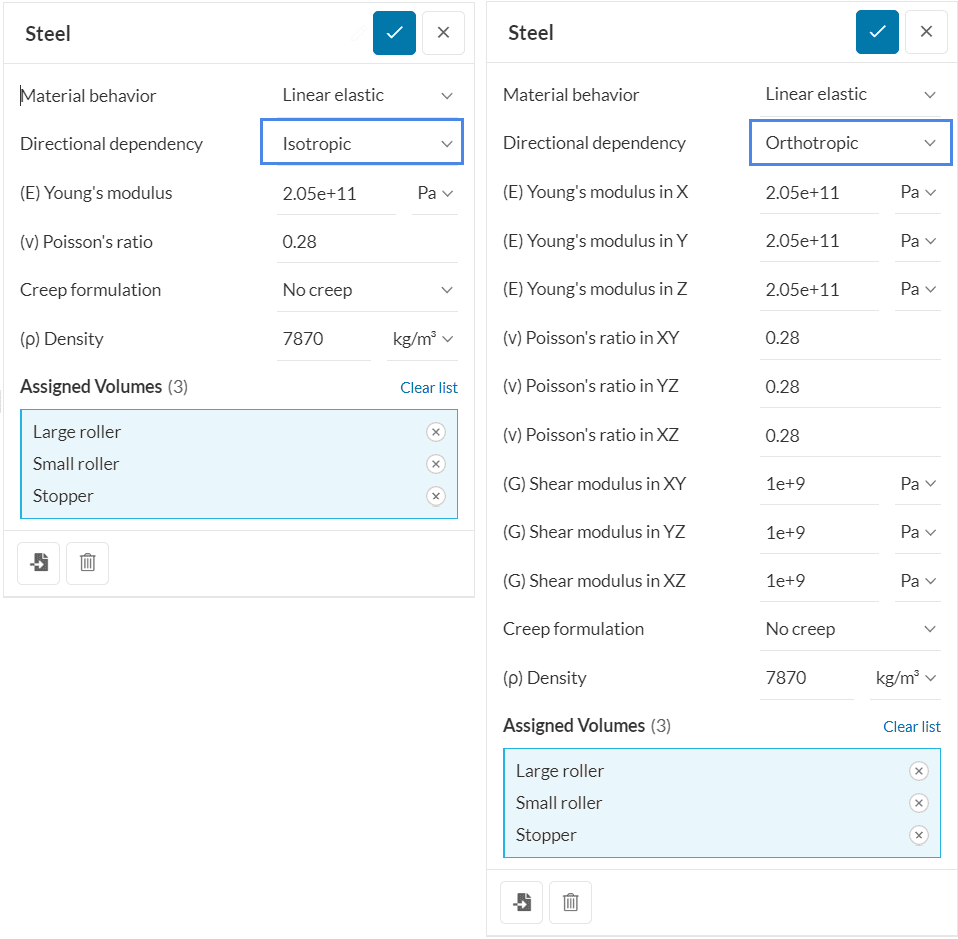
ワークベンチのセットアップ
材料特性は等方性または直交異方性で定義することができます。
線形弾性材料の詳細については、こちらのドキュメントを参照してください:
非線形材料のヤング率
一般的に、すべての固体材料は線形弾性ではありません。図 2 は一軸引張試験で得られた炭素鋼材の応力-ひずみ曲線の例です:
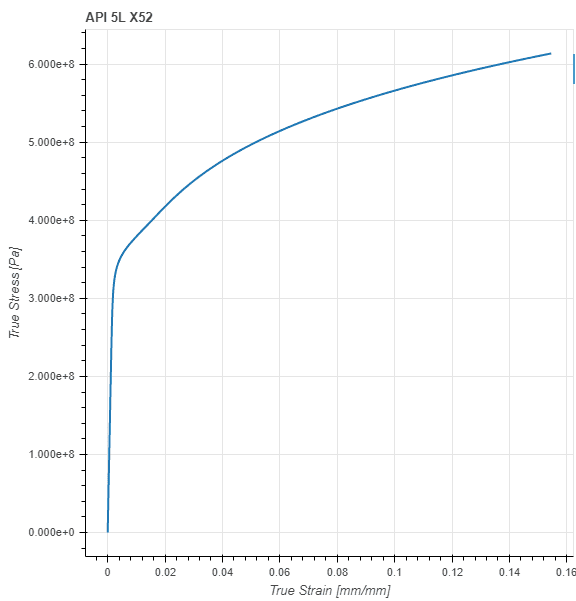
この材料は小さなひずみ値に対してのみ線形弾性挙動を示すことがわかります。変形が大きくなると、非線形挙動が起こり始めます。この場合、延性材料は塑性を示しますが、超弾性や脆性破壊のような他の非線形性挙動も起こり得ます。
一般に、ほとんどの材料は、変形が小さいという仮定の下で、線形弾性と近似することができます。その場合、弾性率は応力-ひずみ曲線の線形部分を解析して計算することで近似できます:
$$ E_y = \frac{ \sigma_y }{ \epsilon_y } $$
ここで
- \( E_y \) :線形弾性ヤング率近似値
- \( \sigma_y \) :弾性限界(直線の端)における応力値
- \( \varepsilon_y \) :弾性限界におけるひずみ値
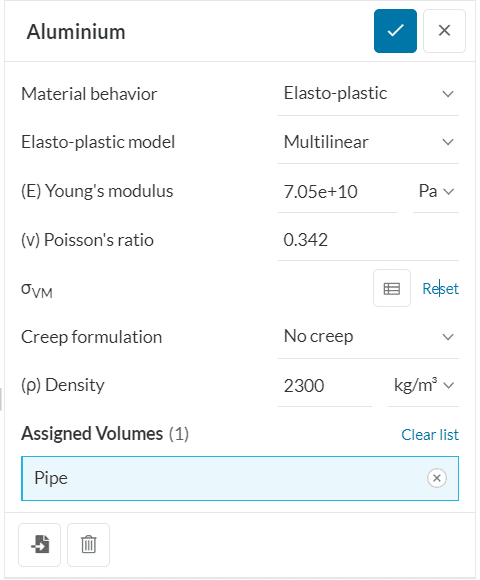
ワークベンチのセットアップ
構造解析をセットアップする場合、弾塑性材料のヤング率は以下のように指定する必要があります:
弾塑性材料の詳細については、こちらのドキュメントを参照してください:
結論として、次のことが言えます。
- 線形弾性 : 弾性率は、上記のように応力とひずみの比例関係を決定します。
- 弾塑性 : 弾性率は、応力-ひずみ状態が降伏点以下の変形曲線の直線部分を決定します。材料がこの閾値を超えると、塑性変形が支配的になります。
最終更新日:2025年1月6日